November 21, 2016 feature
Your brain on math: Functional coupling between neural regions during mathematical cognition
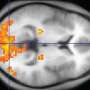
(Medical Xpress)—While human infants, nonhuman primates and birds are capable of approximating or comparing rough arithmetic quantities, post-infant humans are unique in possessing precise mathematical cognition. Historically, what is known as the Triple Code model of numeric processing has hypothesized that symbolic, verbal, and abstract processing – for example, simple visual recognition of a numeral, determining the larger of two numerals, and verbal naming of a numeral, respectively – occur in well-defined coupled brain regions, all or some of which interact. Recently, however, scientists at Baylor College of Medicine, Houston employing electrocorticography (ECoG) electrophysiological recording – in which electrodes are placed directly on the exposed surface of the brain's cerebral cortex – not only reconfirmed math-selective hubs within the lateral parietal cortex (LPC) and ventral temporal cortex (VTC), but more significantly found what they describe as a remarkable diversity of neural responses within each region at both millimeter and millisecond scales. The researchers suggest that numerical processing involves multiple bidirectional functional loops in these, and perhaps nearby, sites – and while acknowledging that their new model does not take other brain regions into account (such as frontal lobe or subcortical structures like the thalamus or basal ganglia) that are likely to be involved in numerical cognition, it may serve as a framework for future mathematical cognition studies.
Dr. Amy L. Daitch, a postdoc in Dr. Josef Parvizi's lab at Stanford University, discussed the paper she and her co-authors published in Proceedings of the National Academy of Sciences of the United States of America. "Our main challenge in measuring lateral parietal cortex (LPC) and ventral temporal cortex (VTC) neuronal electrophysiological activity using direct intracranial electrocorticography recordings was finding neurosurgical cases that had ample coverage in one or both of these regions," Daitch tells Medical Xpress. "It's very rare to find simultaneous recordings from neuronal populations in the human lateral parietal cortex or the ventral temporal cortex," Daitch continues, "because these two regions are less frequently implanted in neurosurgical patients. More importantly, arithmetic tasks during mathematical cognition experiments engage only a few smaller regions within the LPC and VTC."
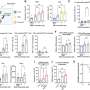
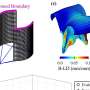
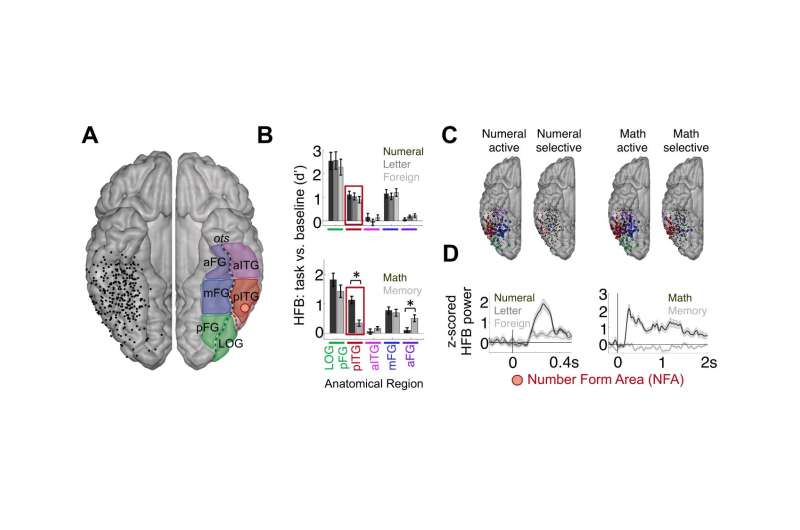
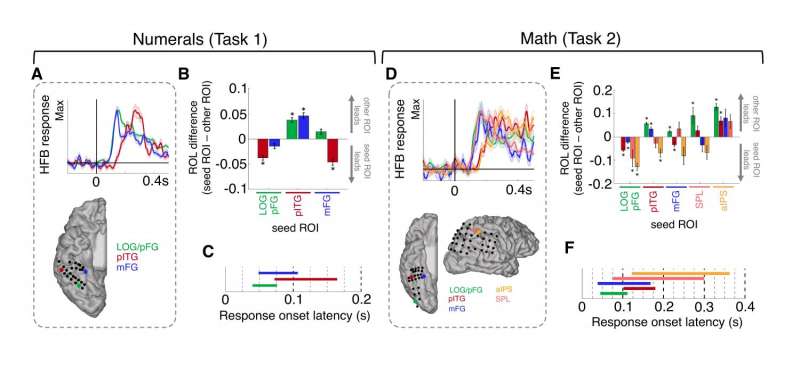
The researchers focused on the significant heterogeneity of responses within a small anatomical area, demonstrating that electrodes 5mm apart may show widely different response profiles – meaning that a single electrode in each of the two areas studied – LPC and VTC – will not provide the selective response data required. In fact, Daitch recounts, due to the rarity of LPC and VTC implantations and as well as sparseness of activity during arithmetic tasks, it took the team several years to assemble their group of subjects, or cohort.
On the other hand, intracranial EEG signals have a high signal-to-noise ratio (SNR) of 100-300% increased power compared to baseline. This allowed the scientists to measure an individual's neuronal population activity without averaging the signal across individuals. "By profiling activity patterns in different VTC and LPC subregions, we were able to report unique timing and selectivity of response profiles across VTC and LPC subregions," she explains. "We could see how neuronal population activity unfolds in these two regions during simple arithmetic tasks, as well as review the profile of responses across tasks at an individual VTC site and see how it predicted its functional coupling with the LPC site." For example, Daitch recounts, the researchers found that the selectivity of a VTC site to math processing was predictive of its degree of coupling with the specific LPC neuronal population that also had selective responses during the arithmetic task, and that the response profile of this VTC site was predictive of the direction of its coupling with the LPC site.
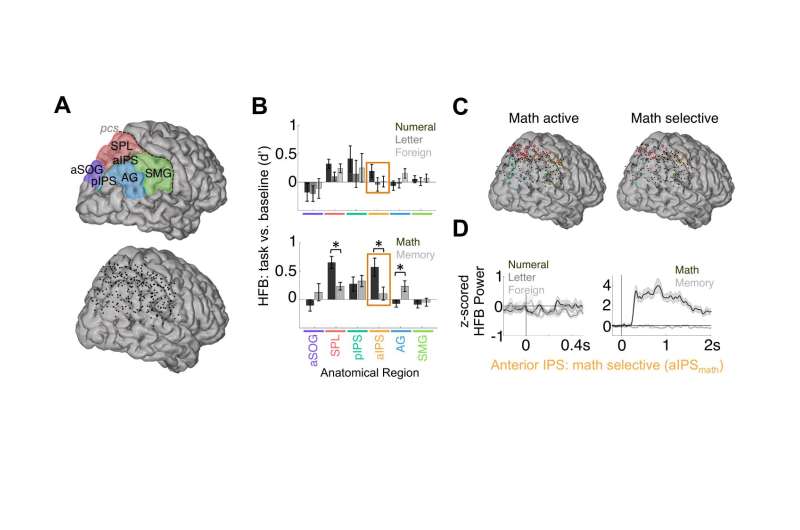
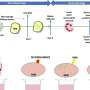
The study's results suggested the presence of what appears to be a temporally- and functionally-synchronized and anatomically selective numerical cognition system. "Just as language processing is associated with a brain network engaged during different aspects of language – for example, visual, semantic and phonetic components – we've identified a brain network for numerical cognition which appears to be involved in processes such as the visual recognition of numerals and arithmetic computations." Daitch explains. She notes that the posterior inferior temporal gyrus (pITG) region of the VTC, which is selective to numerical/mathematical processing, is anatomically distinct from other VTC regions that may be selective for the processing of letters and words, and moreover exhibited anatomically selective functional coupling – during both mathematical tasks and at rest – with an area of the parietal lobe associated with processing quantity. "These results," she underscores, "are in line with the theory that the intrinsic connectivity of brain regions is directly linked to their ultimate functional selectivity. "
One of the study's key findings was the observation of functional millimeter- and millisecond-scale heterogeneity within the LPC and VTC regions. "The temporal and spatial specificity afforded by intracranial recordings allowed us to identify heterogeneity within this numerical cognition network in terms of the engagement of specific neuronal populations during different stages of numerical processing," Daitch says. "Different regions of this network – and even different sites within the same general anatomical region – were engaged at different times during mathematical computations, which suggests that they are involved in different stages of numerical processing." As a result, the scientists conclude that future studies with behavioral paradigms that better isolate distinct processes within numerical cognition will allow them to further refine the fine-grained functional architecture of this network.
Relatedly, the researchers found empirical evidence of functional coupling between the LPC and VTC during mathematical cognition. Theories of numerical cognition (for example, the Triple-code model, which postulates that the human brain contains three different numerical representations – symbolic, verbal, and abstract quantity – each coded in a different brain region) predicted an interaction between VTC and LPC subregions during mathematical processing. In a significant finding, the researchers provided the first empirical evidence of this hypothesis. Importantly, though, this coupling was not purely feedforward from the VTC to LPC as many theories predicted. Rather, heterogeneous subpopulations within the VTC and LPC appeared to be engaged in distinct bidirectional loops between these regions during different stages of arithmetic computations.
"Importantly, the specific functions of the LPC vs VTC in numerical cognition are not as clear cut as previously thought," Daitch points out. "For example, many sites within the VTC do not appear to be involved in the visual recognition of individual numerals, but are rather only active during arithmetic computations. While it therefore appears as if this numerical cognition network as a whole is engaged during many mathematical processes, further work is needed to determine whether different regions within this network do indeed have distinct functions within numerical cognition, and if so, what they are."
Medical Xpress asked Daitch if there might be potential value in determining the relative evolutionary appearance of the brain regions involved in numerical cognition. (For example, the region involved with abstract numerical processing may be assumed to have appeared first due to its (1) quasi-isomorphic mapping of the equal number of real-world objects and (2) presence in nonhuman primates). "According to the Neuronal Recycling Hypothesis1 – which posits that cultural inventions invade evolutionarily older brain circuits and inherit many of their structural constraints – brain regions within the VTC that are selective for words or numbers may be taking over regions that are inherently selective for combinations of line segments and curves (which make up numbers and letters in most languages). The anatomical consistency of the number form and word form area within the VTC is further thought to be driven by the intrinsic connectivity of each of these areas with other brain regions, like the IPS which is thought to code for numerosity for the number form area, and language areas for the word form area", she replied. "Our result showing strong top-down activity from the IPS to pITG supports this idea. However, by recording activity from children as they perform mathematical tasks in future studies, we'll be able to see how math-related regions within the LPC and VTC develop with learning, and which regions exhibit innate selectivity for numerical information prior to learning.
Regarding the potential role of the increasing number and efficacy of cognitive neuroprosthetics in addressing neurological conditions leading to compromised numerical processing capabilities, Daitch is "hopeful that the knowledge gained about the neural mechanisms underlying numerical cognition in healthy subjects may lead to the development of treatments for people with compromised numerical processing abilities. For example, neuroprosthetics may be able to modulate the activity in the aforementioned math-related brain regions within the LPC and VTC."
As to the planned next steps in their research, Daitch and her colleagues are designing experiments which better isolate distinct processes within numerical cognition. "For example," she illustrates, "visually recognizing a numeral versus making a quantity judgment on that numeral – for example, if it's greater than a specified quantity. We want to see which brain regions are engaged during different levels of numerical decisions, and compare the interaction between the VTC and LPC during different levels of numerical processing. For example, does simply looking at a numeral or making a visual judgment on a numeral – such as its color – still activate the intraparietal sulcus (aIPS)? Such a finding would be suggestive of an automatic association of a visual numeral with its quantity representation."
The scientists are also interested in studying the activity of the pITG and aIPS across development, as children learn to associate numerical symbols with quantities – specifically, how does the selectivity of the pITG to numerical/math processing, as well as the nature of its coupling with the aIPS, change with development? "While ECoG is not conducive to longitudinal studies, we plan to record from younger children – who are in the process of learning numerical information – to gain insight into the development of this numerical cognition system."
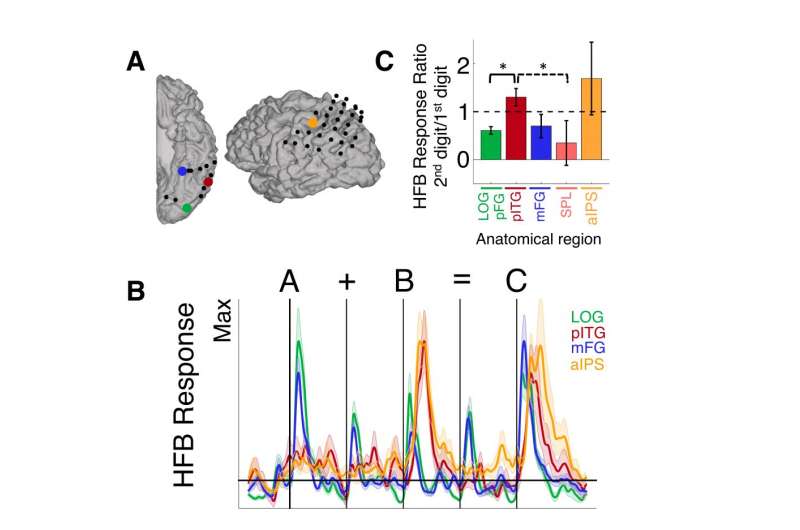
Daitch tells Medical Xpress that there are other innovations they might consider developing. "Since our findings thus far are purely correlative in terms of associating specific neuronal populations with numerical cognition, we would like to apply other techniques, such as electrical brain stimulation (EBS), to gain a better understanding of the causal role of these brain regions in different aspects of numerical and mathematical processing. Targeting different areas – for example, aIPS vs. pITG – with EBS and observing the behavioral effects of each would allow us to better identify the specific functional roles of each region."
Daitch concludes by addressing other areas of research that might benefit from their study. "Many children suffer from dyscalculia," she illustrates. (Dyscalculia is the difficulty performing arithmetic and/or understanding numbers and quantities.) "The neural underpinnings of this developmental disorder are still not well understood. The IPS, which codes for approximate quantity, may be impaired in this population or possibly in the interaction between the pITG and the IPS. We hope that by studying the dynamics of these two regions in subjects with intact math abilities, we will gain insight into the potential neural mechanisms underlying developmental dyscalculia."
More information: Mapping human temporal and parietal neuronal population activity and functional coupling during mathematical cognition, PNAS November 15, 2016 vol. 113 no. 46 E7277-E7286, doi:10.1073/pnas.1608434113
Related:
1Cultural Recycling of Cortical Maps, Neuron 25 October 2007, Volume 56, Issue 2, p384–398, doi:10.1016/j.neuron.2007.10.004
© 2016 Medical Xpress