Mathematicians develop a model of the movement of immune cells
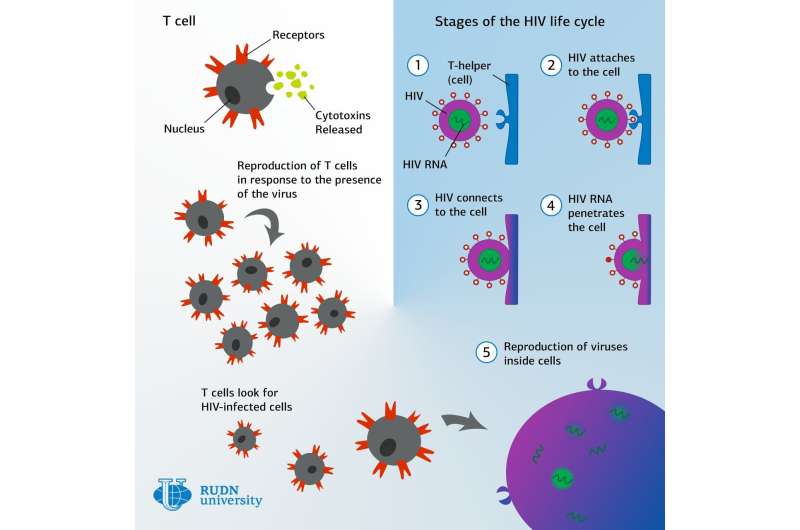
Mathematicians from RUDN University have developed a computational model that allows predicting the mobility of T-lymphocytes, immune cells that recognize and destroy viruses. The model will help in the treatment of immune system disorders, including those that can lead to cancer, and in the development of HIV vaccines. The study was published in Frontiers in Immunology.
Antibodies to HIV infection appear in the body about a month after it has been infected. Prior to that, the immunodeficiency virus can freely circulate and multiply in the body. The vaccine should trigger immune responses at an early stage, when the virus can still be destroyed, or its reproduction effectively restrained. To effectively fight viruses, T-lymphocytes need to find infected cells within 18 hours after they enter the body, before the moment when the viral particles are released from the infected cells and spread.
To create a vaccine, it is necessary to learn how T-lymphocytes move and how they find virus-infected cells. Vitalii Volpert, head of the RUDN University Interdisciplinary Center for Mathematical Modeling in Biomedicine, and his colleagues created a computer model of the movement of immune cells to find out.
Immunologists know that T-lymphocytes move in the intercellular space in search of target cells—that is, cancer cells or cells infected with a virus. To understand how they do it, RUDN University mathematicians created a computer model of the movement of T-lymphocytes.
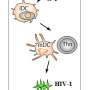
Usually, conditions under which cells exist in the body and the laws of physics that govern them are taken into account for modeling cellular processes. The mathematicians from RUDN University also used real experimental data on the mobility of T cells in their model, among other things. In addition, the model takes into account the interaction of T cells with other cells of the immune system: DC dendritic cells that activate the immune response, CD4 helper cells, and CD8 effector cells that destroy infected cells. To determine how to increase the efficiency of the immune response, the RUDN University mathematicians kept changing the parameters of the model by adjusting the "frequency" of different types of immune cells, that is, the proportion of each type in the population, for example, the proportion of cytotoxic T-lymphocytes that "specialize" in searching for cells infected with HIV.
The mathematical modeling showed that 5% frequency of HIV antigen-specific cytotoxic T cells is sufficient to detect infected cells within 18 hours, before HIV virus particles are released from the infected cells. If the share of cytotoxic T-lymphocytes is increased from 0.04% to 5%, the model shows that the likelihood of detecting HIV-infected cells within 24 hours also increases by roughly five times, from between 7% and 34% to between 84% and 100%.
The results will facilitate the creation of vaccines against HIV, drugs for autoimmune diseases and other disorders associated with immune system dysfunctions. The model helps to predict the effectiveness of the immune response, determines what characteristics of the behavior of immune cells help them to stop the development of the disease, and determines the conditions under which the body can fight the infection before the virus begins to multiply intensively.
More information: Dmitry Grebennikov et al. Spatial Lymphocyte Dynamics in Lymph Nodes Predicts the Cytotoxic T Cell Frequency Needed for HIV Infection Control, Frontiers in Immunology (2019). DOI: 10.3389/fimmu.2019.01213