Network models may help understand spread of new variants in a pandemic

Researchers from Tokyo Metropolitan University have performed numerical simulations based on network theory which show how numbers of infections in a pandemic change when a new variant emerges. They found a non-linear dependence between how infectious the new variant is compared to the existing one, an effect not seen in previous work. Their model may be applied to understand real pandemics such as COVID-19 and inform control measures.

Ever since it began to spread in late 2019, COVID-19 has had a devastating impact on people's lives. With wave after wave of new variants continuing to wreak havoc around the world, scientists have been looking for ways to understand how the disease spreads. In particular, there is the issue of how new variants appear, spread, and end up displacing the existing strain. Understanding the dynamics of variants in a population is vital to controlling their spread.

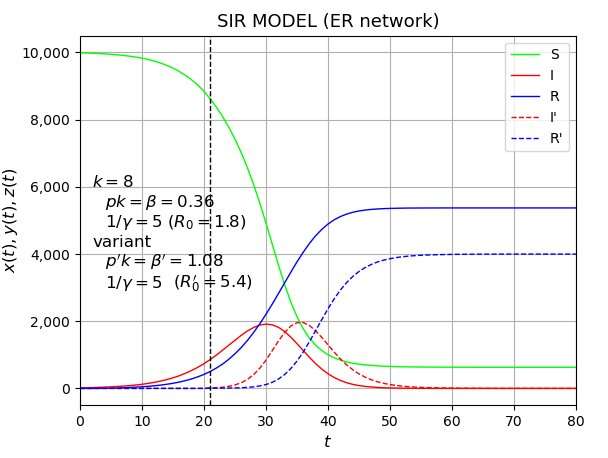
A classic framework for modeling pandemic dynamics is the "compartmental" SIR model, looking at the numbers of susceptible (S), infected (I) and recovered (R) members of a population. The numbers are related by equations and solved, giving many of the salient features of how a disease spreads; the pandemic spreads rapidly before slowing down as the number of susceptible cases decreases and more patients recover. However, the model cannot account for the varied nature of the population, i.e., a given infected individual does not have an equal probability of infecting all others, and the number of contacts that people have can vary greatly from one person to another. Any model that tries to capture pandemic dynamics and get to grips with where and how it spreads needs to use a more sophisticated model.

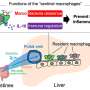
That's why Emeritus Professor Yutaka Okabe and Professor Akira Shudo from Tokyo Metropolitan University have turned to network theory, a mathematical framework that captures how members of a population connect to others. Using different types of networks, they were able to create a more realistic model for how an infectious disease might spread. Key features included dynamic absorbing states, states in which the network can get stuck in over time, e.g., a state with no infected people. With a few infections and low infectivity, the network would collapse back to the infection-free state.

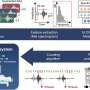
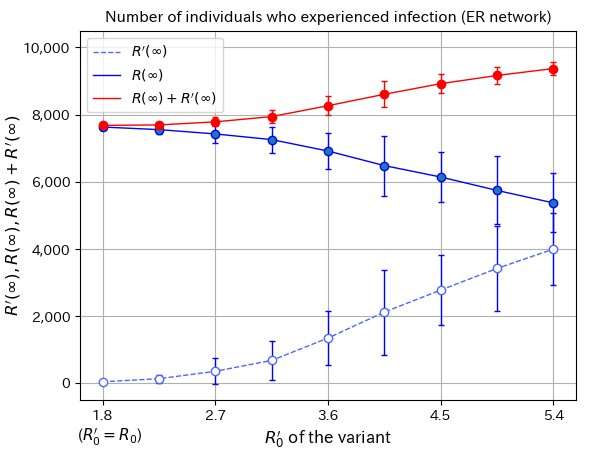
The team performed numerical simulation of the microscopic model on the network; in the middle of a simulation of infectious disease, they added a variant that is more transmissible than the original strain. Looking at the numbers, the team found that a variant with the same infectivity as the existing strain in fact fails to take off at all. This is a direct result of the non-linear nature of the simulation, as the network collapses back to an absorbing state with no infections. As the infectivity of the new variant is ramped up, the population becomes more likely to become infected with the variant as opposed to the existing strain, increasing the rate for the new strain at the expense of the old one. The non-linear nature of how the infection numbers increase with the variant infectivity is a product of the microscopic nature of the network model, giving a more detailed, nuanced picture than before.

The team hopes that their model may be used to form effective strategies to contain infectious diseases, looking at points of significant connectivity in the network and understanding how their isolation affects overall infections. As the COVID-19 pandemic continues to rage, fundamental studies of how diseases spread are a vital piece in informed decision making aimed at bringing normal life back to society.