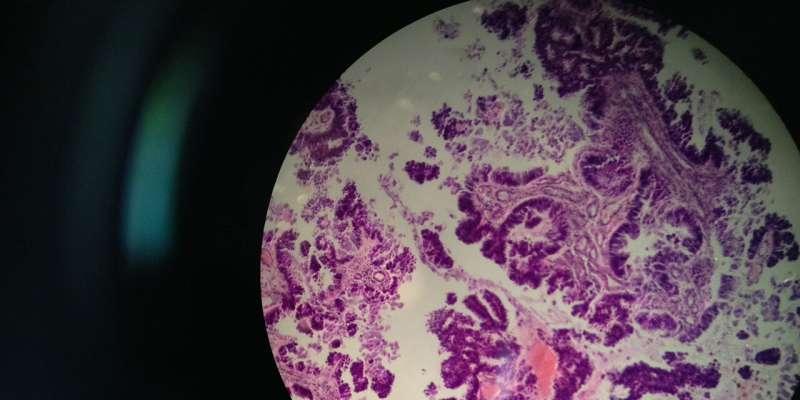
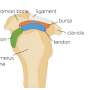
Metastases of a primary intestinal tumor at the level of the brain. Credit: Wikimedia Commons
A new mathematical model uses the size of a cancer patient's initial, primary tumor to predict whether undetectable secondary tumors are already present. Stefano Avanzini and Tibor Antal of the University of Edinburgh, U.K., present the model in PLOS Computational Biology.
As cancer grows, cells can spread from the initial tumor site to other parts of the body and establish secondary tumors called metastases. The presence of metastases is associated with a poorer prognosis and calls for additional treatment. However, very small, early stage metastases cannot be detected by current screening technologies.
For many patients, the primary tumor is surgically removed and no metastases are detected. Avanzini and Antal hypothesized that knowing the size of the primary tumor could help predict the chances that undetectable metastases are already present at surgery. To explore this possibility, they developed a mathematical model of a growing tumor that has an increasing chance to initiate metastases by releasing single "seed" cells, and each of these seed cells has a chance to develop into a secondary tumor.
The researchers used their model to estimate the fraction of patients with visible metastasis at surgery, as well as mean relapse times for several different cancer types. They found that, for typical parameter values, these estimates accurately reflected data from clinical studies.
"We found a wide range of primary tumor sizes for which there were only invisible metastasis predicted. Incidentally, the resected tumor sizes for real patients often fall into this problematic range," Antal says. "Hence, our model predicts that fairly often no metastases are found at surgery, although invisible ones are already there and will relapse in a few years time."
The new model opens up the possibility of quantifying the potential dangers of delays in surgery, which are most critical for smaller tumors that are about to start metastasizing. Future work could extend the model by incorporating more complex aspects of tumor growth.
More information: Avanzini S, Antal T (2019) Cancer recurrence times from a branching process model. PLoS Comput Biol 15(11): e1007423. doi.org/10.1371/journal.pcbi.1007423
Journal information: PLoS Computational Biology
Provided by Public Library of Science