Modeling the past for predicting future COVID-19

Researchers from The University of Alabama, along with international partners, applied a mathematical tool used to model geochemical processes to infections of COVID-19, finding the model can assist in understanding the coronavirus pandemic and evaluating the impact of different mitigation strategies on disease infection.
The team led by Dr. Yong Zhang, associate professor of geological sciences, used a novel fractional calculus technique to model the spread of the coronavirus. He and Dr. Geoffrey Tick, professor of geological sciences, normally apply this math technique to modeling movements of water and pollutants in soil and groundwater.
"COVID-19 spread is analogous to the diffusion-controlled bimolecular reaction, and hence, knowledge learned from the other disciplines may help us understand the spreading of the pandemic," Zhang said. "Many random processes including virus spread, pollutant transport, stock market fluctuation, storm/drought events and even continental drift, although driven by different mechanisms and evolving at different spatiotemporal scales, tend to exhibit similar stochastic characteristics that can be well described by fractional calculus techniques."
In a paper published last month in the journal Chaos, Solitons & Fractals, Zhang, Tick and colleagues from universities and a hospital in China, reported models based on fractional calculus can supplement standard infectious modeling approaches that predict future cases by reproducing infectious spread backwards from current deaths due to COVID-19.
"This model can help us to better understand the nature of real-world processes that have already happened, which, in turn, gives us a better picture of where we are with COVID-19 spread and help predict its evolution into the future," Zhang said.
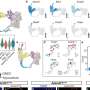
To see how fractional calculus could model the pandemic, the researchers started with China's data from Jan. 23 to March 22, when coronavirus infections peaked, and captured mortality evolution of the virus over the following three months. They found the mathematical model did well in capturing death over time in China, Italy, South Korea and Japan.
The model confirmed strict social distancing can slow the spread of the coronavirus and decrease infections by half, but also found the pandemic will be about two-thirds longer in duration than in scenarios without strict social distancing.
The researchers, however, found the model calibrated with the reported data from China did not do well in matching the evolution of the pandemic as observed over the past three months in the United States and was not reliable at predicting the future evolution of the pandemic because of the unknown maximum number of infections and the widely different mitigation control strategies adopted by the different countries.
For example, the current daily infected population may have reached its peak on April 14 in New York City, resulting in an infection model that may predict the future pandemic under the same conditions. For Montgomery County, Alabama, however, the current infected population has not yet reached its peak, so there are significant challenges and uncertainty for more reliable model prediction, he said.
"It is easy in mathematics to calculate the pandemic status in the next month using our well-validated model," Zhang said. "However, without the ability to appropriately quantify the peak of the current infected population, the model prediction of COVID-19 contains high uncertainty and represents only one scenario of many possibilities into the future."
More data is needed to decrease the model's uncertainty, Zhang said.
More information: Yong Zhang et al. Applicability of time fractional derivative models for simulating the dynamics and mitigation scenarios of COVID-19, Chaos, Solitons & Fractals (2020). DOI: 10.1016/j.chaos.2020.109959