Mathematical constructions of COVID virus activity could provide new insight for vaccines, treatment

Mathematical constructions of the action of SARS-CoV-2 and its multiple spikes, which enable its success at infecting cells, can give vaccine developers and pharmaceutical companies alike a more precise picture of what the virus is doing inside us and help fine tune prevention and treatment, mathematical modelers say.

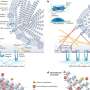
Mathematical construction enables examination of the activity of individual virus particles including the emergence of new spikes—and more severe infection potential—that can result when a single virus particle infects a human cell, says Dr. Arni S.R. Rao, director of the Laboratory for Theory and Mathematical Modeling in the Section of Infectious Diseases at the Medical College of Georgia.

The number of spikes and the way they are distributed on a virus particle are believed to be key in the spread of the virus, Rao and his colleague Dr. Steven G. Krantz, professor of mathematics at Washington University in St. Louis, Missouri, write in the Journal of Mathematical Analysis and Applications.

Laboratory experiments on virus particles and their bonding, or infection, of cells more typically are done on a group of viruses, they write.

"Right now, we don't know when a spike bonds with a cell, what happens with that virus particle's other spikes," says Rao, the study's corresponding author. "How many new infected cells are being produced has never been studied for the coronavirus. We need quantification because ultimately the vaccine or pharmaceutical industry needs to target those infected cells," he says of the additional insight their mathematical methodology, which also enables the study of the growth of the virus' spikes over time, provides.

Viral load is considered one of the strong predictors of the severity of sickness and risk of death and the number of spikes successfully bonding with cells is an indicator of the viral load, Rao says. PCR, or polymerase chain reaction, which is used for COVID testing, for example, provides viral load by assessing the amount of the virus' RNA present in a test sample.

"This is a mathematical analysis that counts the actual number of virus particles, the number of spikes on the viruses and predicts the likelihood of their binding with how many cells," Rao says. "Everything is accountable mathematically, which reduces uncertainty."

They have already used resulting data to create 3D images to better illustrate how spikes diffuse from one organ to another, like from the neck to the lungs.

Math can also enable this kind of detailed insight into specific human populations, like those with comorbid conditions like diabetes and obesity, which are known to typically complicate the COVID course, Rao says.

"We know these patients generally get sicker, but we don't know what is happening inside them with this virus, its spikes and bonding," Rao says. As insight about this infection evolves, it may be that more personalized vaccines and treatments are needed for some of these populations, he says.

Vaccines are designed to destroy the ability of these spikes to bond with cells and even destroy the spikes, Rao and Krantz write. Treatment also can reduce bonding.

The investigators say their mathematical analysis can help vaccine and treatment developers do highly accurate experiments to better understand the role played by the virus' spikes and the impact of current and potential future vaccines and treatment.

This type of detailed mathematical analysis is a new and effective technique for epidemiology, they write.

Not all virus particles present in the body are directly involved in cell infection, and not every spike—a projected 14 to 18 on a single virus particle—is part of an infection when it happens, they say. They also presume that each spike on a viral particle will only infect one cell but that that a viral particle's empty spikes are free to infect other cells.

To infect a cell, spikes connect with ACE-2 receptors on the cell's surface. ACE-2 receptors are found on the surface of many cell types in the body and normally have a role in important body functions like blood pressure control and wound healing. Once inside the cell, SARS-CoV-2 essentially uses the cell's machinery to set up a virus factory, which produces the viral proteins needed to make more virus particles.

Scientists have found that the spikes are both sugar coated, which helps them avoid detection by the immune system, and flexible.