June 28, 2012 feature
Branching out: A mathematical law of dendritic connectivity
(Medical Xpress) -- That the brain is evolution at its finest is perhaps best demonstrated by the beauty, complexity and diversity of dendrites – tree-like structures that form neural circuits by connecting a neuron to its synaptic inputs. Recently, neuroscientists studying the tree-like branching of these diverse structures at Wolfson Institute for Biomedical Research, and the Department of Neuroscience, Physiology, and Pharmacology, at University College London, have derived a surprisingly simple and general equation that directly relates dendrite length with the number of branch points, dendrite spanning volume, and number of synapses. More specifically, they’ve shown that optimal dendritic wiring successfully predicts a 2/3 power law between these three factors. (A power law is a mathematical relationship between two quantities – found throughout the natural world – in which one quantity varies as a power of the other, often identifying simple rules underlying complex structures.) Their theory is both consistent with data gleaned from many types of neurons from a wide range of species yet specific to dendritic trees, leading them to conclude that their findings suggest that there are distinct design principles for dendritic arbors compared with vascular, bronchial, and botanical trees.
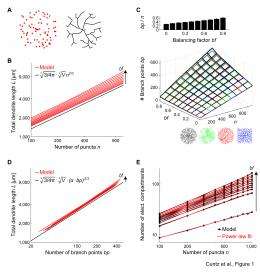
Dr. Hermann Cuntz, working with colleagues Dr. Alexandre Mathy and Prof. Michael Häusser, describes the range of challenges the team faced. “Two years ago we published a method to reproduce dendritic wiring patterns of a wide variety of neurons using computer simulations,” Cuntz tells Medical Xpress. “The paper linked the simple rules of optimal wiring with the actual construction of branching structures. It’s based on the minimum spanning tree, a simple algorithm from graph theory which provides an efficient way to connect a set of targets in terms of wiring cost.” Using this method, the team found it easy to study the relation between parameters of dendritic branching – for example, dendrite length and number of targets - since these factors are parameters of the model. Exploring the model’s parameter space, Cuntz says, he soon found a power law relation between total length and number of targets – and subsequently found the same relationship in all the data from the physical dendrites he tested.
The team’s technical work was based on the development of their universal computer model to simulate dendrite branching structures and the large number of software tools that they published in the TREES Toolbox they created. TREES includes tools to automatically reconstruct neuronal branching from microscopy image stacks; generate synthetic axonal and dendritic trees; edit, visualize and analyze dendritic and axonal trees; exploring how dendritic and axonal branching depends on local optimization of total wiring and conduction distance; and methods for quantitatively comparing branching structures between neurons.
“At this point,” Cuntz continues, “I knew that the dendrites from my computer simulation were based on optimal wiring principles, and that they exhibited a power of around 0.7 between dendrite length and number of branch points and targets. In a hallway conversation with Dr. Mathy – we were both working with Prof. Häusser in London at the time – he and I quickly arrived at a geometrical intuition that predicted a 2/3 power law when optimal wiring conditions are assumed, as we describe in the introduction of our paper. In the meantime we’ve found that a large body of literature in graph theory explores these relations for minimum spanning trees. However, our final equation that links total dendrite length, number of branch points, number of synapses, and volume that the dendrite spans was entirely novel and provides important new insights for neurobiology.” The equation is particularly interesting since these four parameters are among the most important features that neurobiologists and neuroanatomists measure when studying dendrite morphology.
“At this point,” Cuntz adds, “it was fairly easy to demonstrate that our equation holds for a wide variety of dendrites for a number of reasons. First of all, the relation is universally present in all datasets that we analyzed. Secondly, our analysis was made easy by the fact that a group led by one of the founders of the field of Neuroinformatics, Prof. Giorgio Ascoli, has collected a large amount of data from many different labs describing the tree structures of axons and dendrites in NeuroMorpho” (a centrally curated inventory of digitally reconstructed neurons) “ranging from insects to humans and covering a wide variety of neuronal types.” Finally, taking advantage of the TREES Toolbox software package that they’d developed, it was possible to rapidly and interactively analyze great numbers of dendrites and axons in terms of their power law relation.
The scientists are also seeking to improve their theoretical framework. “One prominent open question which we address briefly in our paper,” explains Cuntz, “is whether our model’s assumed dendritic tree targets correspond to synapses made with other dendrites. If so, we make a clear prediction about the relation between the number of synapses and number of branch points and dendrite length.” To that end, they focus on data, from a group led by Prof. Adi Mizrahi, which contains information on dendrite tree structures and locations of presumed synapses in maturing neurons of the olfactory bulb. “In that particular case the targets used for the computer model seem to match the synapse locations measured by Prof. Mizrahi.” On the other hand, Cuntz points out, it’s clear that not all synapses in all systems correspond to such morphological carrier points. “It will be interesting to study which synapse types are the ones which are responsible for shaping the dendrite and what are their distinct features.”
In terms of next steps in their research, Cuntz is investigating a number of parallel paths. “Firstly, one question that remains after concretely relating dendrite structure and optimal wiring is how the dendrite growth process during development implements optimal wiring rules.” To study this, he is collaborating with a number of laboratories that study dendritic growth with genetics and molecular techniques in conjunction with time-lapse imaging, thereby allowing him to follow morphological changes a single neuron undergoes on consecutive days. “Secondly,” he continues, “having an explicit framework to describe dendrite morphology, I can study the consequences for computation and even take advantage of simulated dendritic trees for the use in larger scale realistic neuronal network simulations. To that end, it has recently become evident that the dendrite shape matters for the computations performed on the inputs that a neuron receives. However, no good formalism existed to describe the shape of dendrites. Now that we’ve uncovered a simple and good formalism, it opens up the possibility of studying the relation between dendrite shape and computation in a parameterized and objective manner.”
Cuntz also explicates their finding that implies fundamentally distinct design principles for dendritic arbors compared with vascular, bronchial, and botanical trees. “In a number of landmark papers, Prof. Geoffrey West from the Santa Fe Institute has previously shown that a link between the fractal structures of, for example, vascular and bronchial tree structures and their drive toward efficient flow or distribution of resources explains a number of power law relationships between their branching parameters. However,” Cuntz stresses, “we’ve shown that the fractal structures of dendrites and axons are fundamentally distinct from those of vascular and bronchial trees. We calculated that the power law relation expected from the West model would be 4/3, which is very different from the 2/3 that we find for dendritic trees. Specifically,” he stresses, “the fact that 2/3 is less than 1 means that, proportionally, the more synapses/branch points we add within a given space, the less we need “cabling” to connect them – but also, the less computational units you get.” He notes that this may be related to the fact that the function of dendrites is arguably not to distribute resources, but rather to perform computations on their inputs while preserving conduction times and material costs.
Looking beyond his immediate area, Cuntz reflects on one of the grand mysteries in the field of brain science is – namely, what are the basic elements of computation in the brain? “This question goes beyond neuroscience, since computation is increasingly relevant in our everyday life. Our findings reveal a constraint to computation in the single neuron since we show that the 2/3 power between synapse number and dendrite length extends to its electrical compactness, and the number of computational units within one dendrite. This means,” Cuntz concludes, “that there’s a 2/3 power between the number of synapses and that of computational compartments – an interesting scaling property that directly affects computation in the brain.”
More information: A scaling law derived from optimal dendritic wiring, PNAS published online before print June 19, 2012, doi: 10.1073/pnas.1200430109
Related: One Rule to Grow Them All: A General Theory of Neuronal Branching and Its Practical Application, PLoS Computational Biology 6(8): e1000877, August 5, 2010, doi:10.1371/journal.pcbi.1000877
Copyright 2012 Medical Xpress
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.