New discovery in connectome dynamics

From diffusion tensor imaging data of the Human Connectome Project, it is possible today to construct hundreds of graphs mapping the cerebral connections of a human subject. Each of these graphs has 10¹⁵ vertices and several thousand edges.

In applications of the graph theory, it is unusual to find numerous, pairwise graphs on the same set of vertices. In the case of human braingraphs or connectomes, however, this is the standard situation: The nodes correspond to anatomically identified cerebral regions, and two vertices are connected by an edge if a diffusion MRI-based workflow identifies a fiber of axons running between the two regions corresponding to the two vertices. Therefore, if the brain graphs of n subjects are examined, then n graphs on the very same, anatomically identified vertex set are considered. It is a natural idea to describe the k-frequently appearing edges in these graphs— the edges that are present between the same two vertices in at least k out of the n graphs.

Based on the NIH-funded Human Connectome Project's public data release, the mathematicians of the PIT Bionformatics Group of the Eötvös University previously reported the construction of the Budapest Reference Connectome Server that generates and visualizes these k-frequently appearing edges. The graphs of the k-frequently appearing edges are called "k-consensus connectomes,'' since an edge could be included if and only if it is present in at least k graphs out of n.

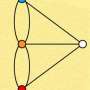
When viewing k-consensus connectomes for a large k, and then decreasing the value of k one by one while approaching 1, more and more edges appear in this graph.

Astonishingly, the new edges do not appear randomly in the braingraph—they appear as the branches of a tree or a shrub grow: the new edges are usually connected to the older ones.

This phenomenon is illustrated here—after selecting "show options," move the "minimum edge confidence" slider from right to left to see the newly appearing edges.

The scientists hypothesize that the phenomenon that they call "consensus connectome dynamics" describes the development of the connections in the human brain: the k-consensus connectome for k=n (that is, for all subjects) contains connections that are present in all subjects, and these connections were established during brain development, and for decreasing k values, more and more edges appear as the small individual differences summed up in the axonal development. If the hypothesis is correct, then the phenomenon makes possible the assignment of directions to the connections. Directing of the graph edges, determined by diffusion tensor imaging, were not possible before.