How mathematics is helping to fight cancer

Nearly half of Canadians will develop cancer in their lifetime, according to the Canadian Cancer Society. Globally, cancer is the second leading cause of death.
When cancer emerges in the human body, it results in cells that are "aggressive" and able to evade the body's growth control mechanisms. These cells are also "invasive," entering and subsuming adjacent tissues. And they are often "metastatic" —travelling to and colonizing distant sites in the body.
One of the greatest unsolved challenges in cancer treatment concerns the frequent relapse of patients being treated by chemotherapy, and the emergence of chemotherapeutic resistance in cancers.
At the Mathematical Medicine Group at the University of Waterloo, we have been applying mathematical and computational approaches to understand cancer growth and control for more than a decade now. Working together with cancer biologists and clinical oncologists, we try to understand some of the challenges in cancer treatment, including drug resistance and relapse.
Mathematical models allow us to quickly search and identify the most effective drug combinations for cancer patients. They are also deepening our understanding of how and why cancer cells often become resistant to chemotherapy drugs.
We believe that this growing interaction of mathematical scientists with cancer biologists and clinical oncologists will also lead to many future advances and breakthroughs in cancer treatment.
The challenge of drug resistance
The standard treatment for most cancers involves a combination of surgery and chemotherapy and/or radiation therapy.
Chemotherapy drugs have, by and large, proved effective in destroying cancer cells by preventing them from growing and dividing. But they are clearly a "double-edged" sword as they destroy, and cause mutations in, healthy, normal tissue cells.
And patient survival doesn't just depend on eliminating cancer cells. We also need to control or overcome drug resistance. Every year thousands of patients die from recurrent cancers that have become resistant to chemotherapy.
Combination therapy is one very promising strategy. But this raises its own questions —about how to administer the drugs, which can be combined in a seemingly infinite order and sequence.
Mathematical models can be used to study these types of questions, offering the cancer biologist and clinical oncologist powerful new tools to add to their arsenal of laboratory and clinical approaches.
These models offer a rational and unique method of searching through a large number of possible strategies to identify the most efficient doses to extend patient survival.
Chemotherapy itself causes resistance
Our team is currently focused on developing a deeper understanding of how cancer cells become resistant to chemotherapy drugs, leading to relapse.
By integrating math with computational and experimental studies, we try to understand and unravel how particular combinations of drugs can help to overcome this resistance.
Not all cancer cells are born equal. They compete with each other and the ones that survive pass on genetic information to their daughter cells.
The lack of uniform characteristics among cellular populations has been identified as an important factor which complicates and impedes treatment response in a number of tumours. We have two competing theories to explain this: 1) the standard theory of "clonal evolution" and 2) the "cancer stem cell hypothesis."
The theory of clonal evolution states that most tumours arise from single cells through the accumulation of many genetic changes.
However, the cancer stem cell hypothesis suggests that only a sub-population of so-called "cancer-initiating cells" have the capacity for unlimited cell division and therefore drive tumour growth. These cells are very aggressive, less sensitive to drugs and appear to be the driving force of metastasis (the spread of cancer cells to distant sites) which frequently results in patient death.
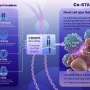
Our team has published papers in Nature Communication and ACS Nano, in collaboration with two cancer biologists at Harvard Medical School —Dr. Sengupta and Dr. Goldman—to show that non-cancer stem cells can also become resistant to chemotherapy drugs.
This means that resistance can be acquired as a direct result of chemotherapy. It challenges the current explanation that resistance is innate or acquired as a result of random mutations.
Inspiring nanomedicine
We have also used mathematical modelling, integrated with experimental data, to understand the chemo-resistant characteristics of cancer cells and how they survive treatment over time.
Using mouse models of aggressive breast cancer, we have confirmed the predictions from our mathematical model that, to overcome resistance and relapse, a lethal combination of drugs in a single nanoparticle (a tiny particle) must be delivered to the same cell.
These recent papers highlight the importance of mathematicians and cancer biologists working together. They show math can help understand cancer and also have a profound impact on therapy outcomes.
Mathematical and computational strategies provide a painless, fast and cost-effective way of testing different drug combination strategies, as well as other hypotheses using computational models.
Math can even inspire the design of nanomedicine.
This article was originally published on The Conversation. Read the original article.![]()