Mathematicians develop model of spatial distribution of HIV and other viruses in the body for the first time

RUDN mathematicians created a mathematical model to describe spatial distribution of viruses in the body. It analyzes the growth of a virus population in space and time and evaluates the influence of their reaction with the immune system on the course of the disease. The results may be useful for the diagnostics and control of HIV, herpes, myxovirus, measles and other viral diseases. The article was published in the Journal of Theoretical Biology.

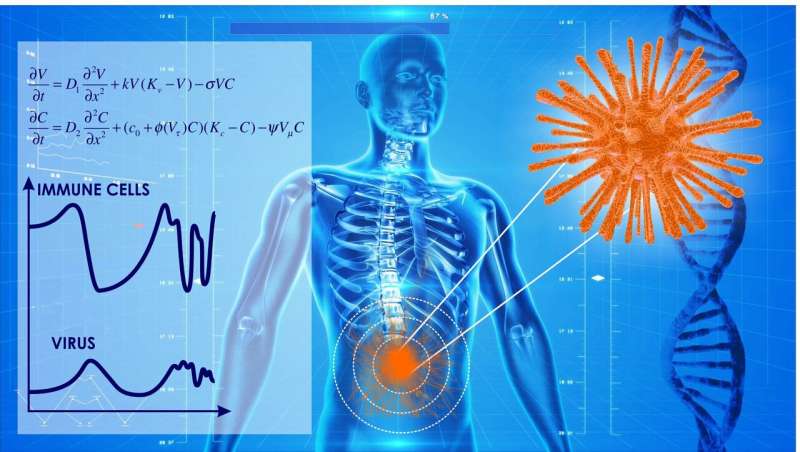
Combating HIV requires detailed understanding of how the infection spreads in the body. Although there are many models describing the intercommunication between HIV and a cell, each of them contains approximations that affect complete understanding of the infection's development. RUDN medics and mathematicians developed a new model—unlike previous ones, it takes into consideration spatial distribution, an important aspect of virus-cell reactions. The model broadens earlier ones and is represented by a system of differential equations that describe the evolution of a virus population and immune system cells in space and time. Moreover, the model is applicable to other viral diseases as well.

When a viral infection enters a body, it causes an immune response aimed at its destruction. However, there are certain viruses the system is unable to tackle, including HIV. It chooses T-lymphocytes as its host cells. In a healthy body, they would either destroy an infected cell or activate other cells able to kill it. HIV kills T-lymphocytes, and their number gradually reduces until the immune system is unable to fight an infection agent. This leads to AIDS, the last stage of HIV.

The researchers identified three possible ways for an infection to develop: treatable infections, chronic subinfections, and chronic strong infections. In the first case, an infection can be completely destroyed; in the second one, it remains in the body together with a chronic immune response. In the third, immune cells wear out, inflicting high viral load on the body. The authors carried out detailed analyses of each result and found a correlation between the distribution of a viral infection and the virus-cell intercommunication.

"From the point of view of mathematical modeling, the distribution of infection in a cell culture or tissue is described by solutions similar to a progressive wave of reaction-diffusion equations. We've studied this issue, taking into account the intercommunication between a viral infection and immune cells. It occurs when viruses are able to infect immune response cells (lymphocytes) and reproduce in them. HIV is one example of such a virus, but they also include herpes, myxovirus and measles," said Vitaly Volpert, the author of the article, and the head of the laboratory of mathematical modeling in biomedicine at RUDN.