A mathematical model to help optimize vaccine development
When it comes to the design of a novel vaccine against viral infection, vaccine developers have to make several major decisions. One of them is the choice of what type of immune response they wish to induce.
In a recent Forum article in Trends in Immunology a group of researchers at UPF and the Marchuk Institute of Numerical Mathematics in Moscow, Russia, led by Andreas Meyerhans and Gennady Bocharov, provides a theoretical paper that might help with this issue. The researchers have used a mathematical model to better understand the immune response to vaccines. This could help improve vaccine design and simplify the associated technical challenges.
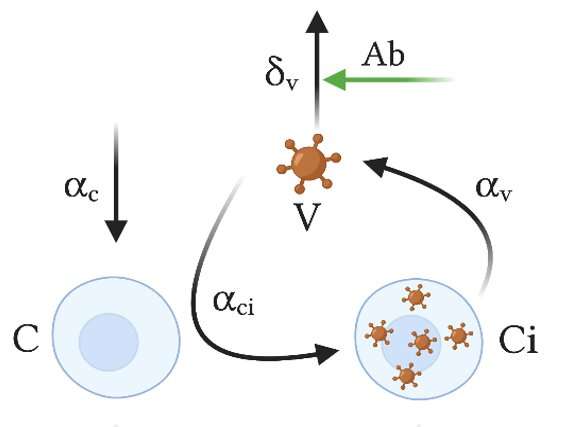
Viruses are intracellular parasites that need host cells to multiply. Thus, for a virus to infect a human, it has to get access to some of the body's cells that will enable viruses to multiply. Progeny viruses will be assembled within the infected cells and, upon release, will infect other target cells in the surroundings. Without any immune response to counteract the virus, it will continue to spread and may cause organ damage.
The researchers have used a mathematical model to better understand the immune response to vaccines. This could help improve vaccine design and simplify the associated technical challenges.
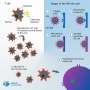
Vaccines are the most cost-effective way to provide a host with virus-specific immunity that will then help it to keep an infectious virus below pathogenic levels. To do so, vaccines may induce antibodies that help to neutralize assembled free viruses and virus-specific cytotoxic T cells that will kill infected cells and thus reduce the number of virus-producing cells.
While both arms of the immune response are considered of major importance for vaccine efficacy, the question is how do they cooperate? Are their actions simply additive or more than additive? The researchers have now addressed these fundamental questions by examining the contribution of antibodies and cytotoxic T cells using a model based on virus infection dynamics. They show that these two primary control factors of virus infection are cooperating multiplicatively rather than additively. While this relationship might appear rather abstract, it has very practical consequences for vaccine development.
For example, f to be efficient a virus vaccine needs to increase the basic immune response by a factor of 10,000, this may be achieved in two ways. Either antibodies or cytotoxic T cells are increased by a factor of 10,000 or each of these responses is increased by only a factor of 100. The latter might be easier to obtain in practical terms and thus provide vaccine developers with different options for their design.
Although these considerations are based only on theoretical grounds and require experimental validation, the first data in this direction are emerging. "We hope that our conceptional work will positively help with vaccine design," says Bocharov. And Meyerhans, the last author of the study, adds that "our considerations may help to simplify the technical challenges for novel vaccines and thus be of some practical use for healthcare."
More information: Gennady Bocharov et al, Examining the cooperativity mode of antibody and CD8+ T cell immune responses for vaccinology, Trends in Immunology (2021). DOI: 10.1016/j.it.2021.08.003